En estas páginas estudiaremos los procedimientos numéricos para hallar las raíces de una ecuación trascendente, y para hallar las raíces de un polinomio. El cálculo de las raíces de un polinomio puede efectuarse con los mismos procedimientos que para una ecuación en general, sin embargo, aprovechando las propiedades de dichas raíces se elaboran métodos específicos para este tipo de ecuaciones. Entre estos últimos, hemos de destacar el método de Graeffe muy apropiado para ser codificado y usado en los ordenadores.
En las primeras páginas, describiremos dos procedimientos para obtener las raíces de una Ecuación trascendente: el método de las aproximaciones sucesivas y el procedimiento del punto medio. Existen otros procedimientos como el gráfico, de las partes proporcionales, el método de las tangentes o método de Newton. Cada procedimiento tiene, sin duda, sus ventajas e inconvenientes, e incluso se pueden combinar varios procedimientos a la vez.
El procedimiento gráfico consiste en representar la función en un intervalo dado y observar cuantas veces cruza el eje X en dicho intervalo. Si el eje X está convenientemente etiquetado y la resolución es suficiente, este procedimiento nos da una primera aproximación a las raíces de la ecuación.
- Raíces simples
- Raíces múltiples
- El pozo de potencial
Los procedimientos iterativos son muy importantes en el cálculo numérico, y consisten en repetir la misma rutina una y otra vez hasta que se cumpla una determinada condición de terminación del proceso de iteración. Estos procedimientos son muy fáciles de codificar y se prestan especialmente para ser usados en los ordenadores.
Para hallar las raíces de una función trascendente, crearemos una clase base abstracta con una función miembro que describe el procedimiento numérico, y una clase derivada que definirá la función cuyas raíces deseamos calcular en un intervalo dado. Para calcular las raíces, crearemos un objeto de la clase derivada y llamaremos desde éste al procedimiento numérico, pasándole el principio y final de dicho intervalo.
Para calcular las raíces de un polinomio, crearemos una clase específica, cuyas funciones miembro realizan distintas tareas, entre otras las siguientes:
- Calcular las raíces reales simples
- Calcular las raíces reales dobles
- Calcular las raíces complejas en estos dos casos:
- cuando el polinomio tiene una raíz compleja y su correspondiente conjugada
- cuando el polinomio tiene dos raíces complejas y sus correspondientes conjugadas.
OTROS MÉTODO
MÉTODO DE NEWTON - RAPHSON
Supongamos que tenemos la aproximación 
a la raíz 
de 
, Trazamos la recta tangente a la curva en el punto 
; ésta cruza al eje 
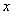en un punto 
que será nuestra siguiente aproximación a la raíz 
. Para calcular el punto 
, calculamos primero la ecuación de la recta tangente. Sabemos que tiene pendiente Y por lo tanto la ecuación de la recta tangente es:
Hacemos 
: Y despejamos 
: Que es la fómula iterativa de Newton-Raphson para calcular la siguiente aproximación:
|  | , si |  |
Note que el método de Newton-Raphson no trabaja con intervalos donde nos asegure que encontraremos la raíz, y de hecho no tenemos ninguna garantía de que nos aproximaremos a dicha raíz. Desde luego, existen ejemplos donde este método no converge a la raíz, en cuyo caso se dice que el método diverge. Sin embargo, en los casos donde si converge a la raíz lo hace con una rapidez impresionante, por lo cual es uno de los métodos preferidos por excelencia.
También observe que en el caso de que 
, el método no se puede aplicar. De hecho, vemos geométricamente que esto significa que la recta tangente es horizontal y por lo tanto no intersecta al eje 
en ningún punto, a menos que coincida con éste, en cuyo caso 
mismo es una raíz de 
!
Ejemplo 1
Solución
En este caso, tenemos que
De aquí tenemos que:
Comenzamos con 
y obtenemos: En este caso, el error aproximado es,
Continuamos el proceso hasta reducir el error aproximado hasta donde se pidió.
Resumimos los resultados en la siguiente tabla:
| Aprox. a la raíz | Error aprox. |
| 1 |
|
| 1.268941421 | 21.19% |
| 1.309108403 | 3.06% |
| 1.309799389 | 0.052% |
De lo cual concluímos que 
, la cual es correcta en todos sus dígitos. Veremos a continuación un ejemplo del metódo de Newton Raphson, con la siguiente ecuación:
X ^ 3 + X + 1 6 = 0
| # | Fxn | Dfxn | Nuevo Xm |
|---|
| 1 | 18 | 4 | -3.5 |
| 2 | 12.5 | 37.75 | -3.8311258278146 |
| 3 | -44.062571359569 | 45.032575325644 | -2.8526658787457 |
| 4 | -10.066812462104 | 25.41310784728 | -2.4565391034374 |
| 5 | -1.2807315732707 | 19.103753100152 | -2.3894982677149 |
| 6 | -0.03282123757409 | 18.129105914238 | -2.3876878509338 |
Hemos terminado de analizar el método de la Newton Rapshon, en este ejemplo con un error de 0.0001; se encuentra la última raiz(Xm): -2.3876878509338 con 6 iteracciones.
, comenzando con 
. 
